1dL(デシリットル)は何mL(ミリリットル)ですか?
このような問題が、小学生の算数の問題で出題されることがあります。
dL(デシリットル)からmL(ミリリットル)のように、同じ数量のものについて単位を換えることを「単位変換」といいます。簡単な単位変換は小学2年生でも学習します。しかし、大人でも「単位変換」を難しく感じる場面は多いのではないでしょうか?
この記事では、そんな単位変換のコツについてわかりやすく解説していきます。dLやmLに限らず、色々な単位に応用できる考え方ですので、是非日々の生活などにお役立てください。
1dL(デシリットル)は100mL(ミリリットル)
まずは、冒頭で紹介した問題の答えを確認しておきましょう。
1dL(デシリットル)は100mL(ミリリットル)
記事冒頭の問題の答えは、ズバリこれです。ここからは、なぜそうなるのかについて考え方を詳しく説明していきます。
考え方はいいから、結果だけを手っ取り早く知りたい!という方は以下の記事がおすすめです。
まずは基本的な単位表記のルールを確認する
まず大切なのは、「基本的な単位表記のルール」を確認することです。
基本的な単位表記のルールというのは、
「大きさを示す記号(SI接頭語)」+「基本の単位」
という形です。まずは、このことをおさえておきましょう。
d(デシ)やm(ミリ)は「大きさを示す記号(SI接頭語)」
d(デシ)やm(ミリ)などは、大きさを示す記号です。このような記号のことを、SI接頭語といいます。SI接頭語は国際基準であり、世界共通です。
SI接頭語は以下のようなものがあります。
- p(ピコ)…\(\displaystyle\frac{1}{10^12}\)
- n(ナノ)…\(\displaystyle\frac{1}{10^9}\)
- μ(マイクロ)…\(\displaystyle\frac{1}{10^6}\)
- m(ミリ)…\(\displaystyle\frac{1}{1000}\)
- C(センチ)…\(\displaystyle\frac{1}{100}\)
- d(デシ)…\(\displaystyle\frac{1}{10}\)
- da(デカ)…×10
- h(ヘクト)…×100
- k(キロ)…×1000
- M(メガ)…×\(10^6\)
- G(ギガ)…×\(10^9\)
- T(テラ)…×\(10^12\)
などがあります。意外と聞いたことのある単位が多いのではないでしょうか?
L(リットル)やM(メートル)などが「基本の単位」
基本の単位というのは、
- 容積を表す L(リットル)
- 長さを表す M(メートル)
- 重さを表す g(グラム)
など、基本となる単位のことです。
この基本の単位に、「大きさを示す記号」(SI接頭語)を合わせることで、様々な単位を表すことができるのです。
単位表記のルールは「大きさを示す記号(SI接頭語)」+「基本の単位」
ここまで「大きさを示す記号(SI接頭語)」と「基本の単位」について説明してきました。ここからは、dL(デシリットル)という単位を例に、単位表記のルールについて考えていきましょう。
dL(デシリットル)という単位は、d(デシ)とL(リットル)で分けて考えます。
dL(デシリットル)の場合、
- d(デシ)が「大きさを示す記号(SI接頭語)」
- L(リットル)が「基本の単位」
です。
SI接頭語のd(デシ)は、\(\displaystyle\frac{1}{10}\)の大きさであることを示すので、1dLは1Lの\(\displaystyle\frac{1}{10}\)つまり、
1dL=\(\displaystyle\frac{1}{10}\) L
であることが分かります。これは、1dLが10コ分で1Lになるということです。
このように、SI接頭語の意味と、基本の単位を知っているだけで、世の中のさまざまな単位を今よりもより理解することができるのです。
- 天気予報などで耳にする気圧の単位hpa(ヘクトパスカル)は、h(ヘクト)とpa(パスカル)
- 騒音などを調べる際に使う音の大きさを表す単位dB(デシベル)は、d(デシ)とB(ベル)
- PCのメモリー容量を表すGB(ギガバイト)やTB(テラバイト)は、G(ギガ)やT(テラ)とB(バイト)
などのように考えれば、単位の意味が今よりもより理解できるようになります。また、この記事のテーマである「単位変換」も比較的わかりやすく考えられるようになるのです。
単位変換のポイントは「基本の単位のどれだけか」を考えること
ここからは、単位変換について解説します。この記事の冒頭に挙げた問題
1dLは何mLですか?
について考えていきましょう。
dLは、Lリットルという単位のdデシ(\(\displaystyle\frac{1}{10}\))を示しますから、
1dLは1Lの\(\displaystyle\frac{1}{10}\)つまり、
1dL=\(\displaystyle\frac{1}{10}\) L
であることが分かります。ここで、mLは 同じくLリットルという基本の単位のmミリ\(\displaystyle\frac{1}{1000}\)を示しますから、
1mL=\(\displaystyle\frac{1}{1000}\)L
です。\(\displaystyle\frac{1}{1000}\)Lがいくつ集まれば\(\displaystyle\frac{1}{10}\)Lになるのかを考えればいいのです。
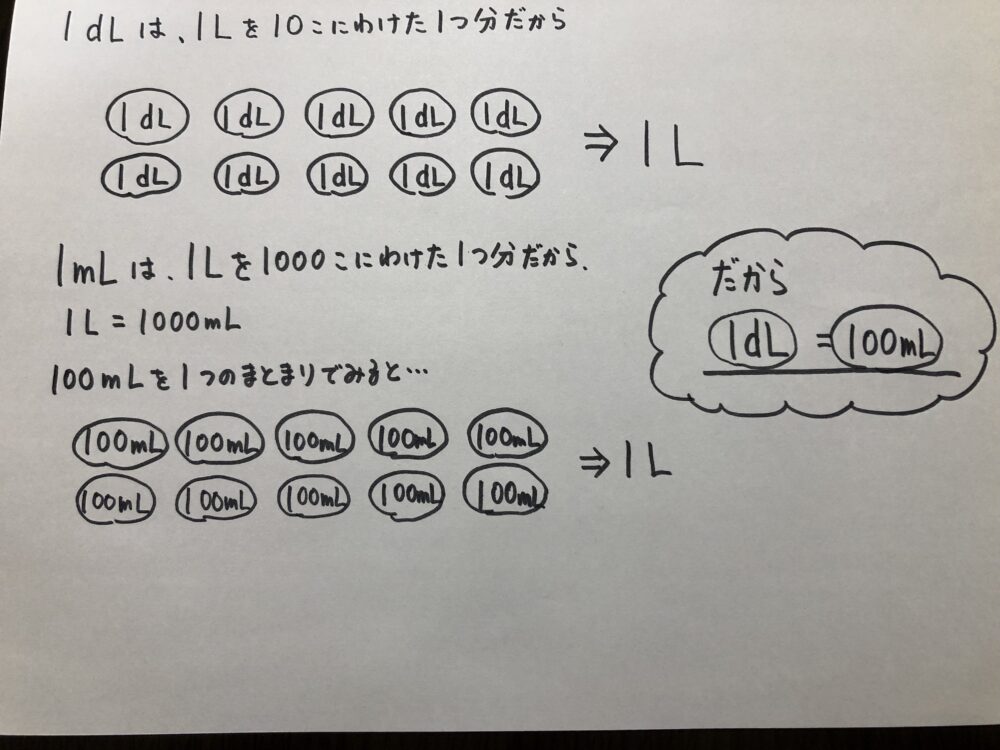
まとめると、上の図のようになります。
答えは、1dL=100mLです。
初めて見る単位でも変換可能になる
このやり方を使うことで、よりわかりやすく単位変換を行うことができます。また、初めて見る単位でも計算が可能になります。
小学2年生で「dL(デシリットル)」を学習することに対して疑問の声も聞かれますが、私はこのような単位変換のルールを知る意味で学習する意味はあると思っています。
ちなみに私がよく授業で取り上げるのは「kL(キロリットル)」です。皆さんはこの表記を見たことがありますか?
私は普段から自動車の運転をよくするのですが、運転をしているとガソリンなどを運ぶトラックにこの単位が記載されています。
k(キロ)は×1000という意味がありますから、1kL(キロリットル)は1000L(リットル)ということになります。
まとめ
単位変換の計算を全て暗記でやろうとしてしまうと大変ですから、単位表記の意味を理解した上で考えてみると良いでしょう。
単なる豆知識として、あるいは学習指導の参考として、この記事が皆様のお役に少しでも立てたら幸いです。
最後までお読みいただきありがとうございました。




