突然ですが、
1÷0=?
の計算の答え、わかりますか?
この計算の答えは「答え無し」です。
学生時代に習った記憶はあるけれど、なぜなのか説明できない、という方も多いかもしれません。
この記事では、「0で割れない(÷0が計算できない)理由」をわかりやすく解説していきます。
÷0を考える前に、×0を考える

÷0が計算できないということを考える前に、×0の計算について考えてみましょう。かけ算というのは、「もとの数がいくつ分か」を表す計算のことですから、
×0というのは、もとの数の0こ分であり、例えば、1×0=0,2×0,10×0=0…
のように、かけられる数がいくつであっても答えはいつも0となります。かけ算の考え方については以下の記事で詳しく書いていますので、もしよければお読みください。
×0の答えがいつでも0になるため、÷0も感覚的に答えがいつでも0になるのでは?と考える人も多いかもしれませんが、そうではありません。
わり算の計算を、具体的な場面で考えてみる
では、÷0の計算の答えを、具体的な場面を例に考えてみましょう。

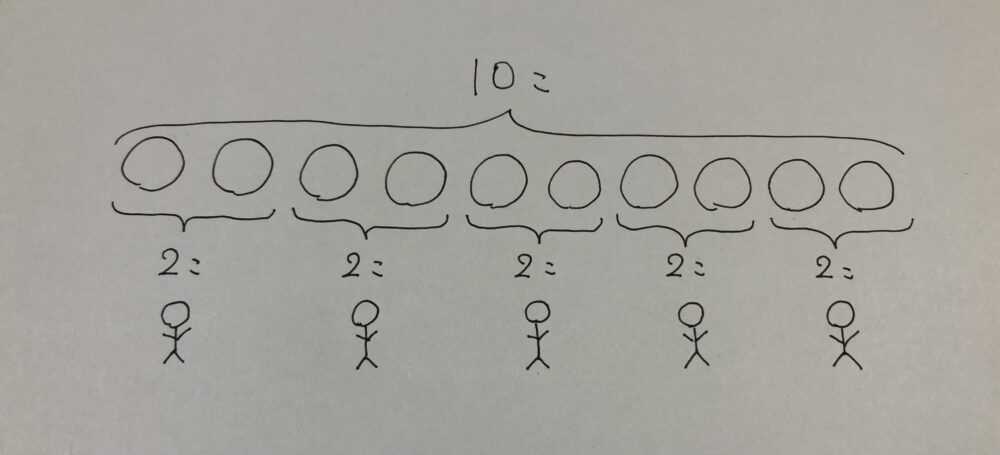
ここでは、わり算を使う場面として「10このものを何人かで均等に分ける」という場面を考えます。キャンディを分けましょうなどの問題がよくありますね。
例えば、5人で分ける場合の計算式は10÷ 5 となります。

この計算を下の図のように考えると、1人あたり2こずつとなりますから、
10÷5=2
という式が成り立つことが確認できます。
÷0の計算は、具体的にどんな場面なのか

では、上の例と同じく「10このものを何人かで均等に分ける」という場面を考えます。ここでは0人で分けることを無理矢理イメージして考えてみましょう。
その場合、計算式は
10÷0
となります。
ここで問題になるのは「0人で分けるとはどういうことか?」ということです。

- 0人で分けるというのは、誰の手にも渡らないから、答えは0…?
- あるいは、分けることにならないから、答えは10…?
このように、場面のイメージだけでは結論は出そうにありません。
そもそも0人で分けるという言葉自体に無理がありますね。
具体的な場面のイメージだけでは、÷0が計算できないことの説明がつかない
このように、具体的な場面のイメージだけでは÷0が計算できないことの説明がつかないのです。÷0が計算できないことを説明するには、別のアプローチが必要です。
ではどうするのか?それには「式の性質」に注目する必要があります。
解決の鍵は、かけ算とわり算の性質
ここで解決の鍵は、「かけ算とわり算の式の性質」です。
2×5=10
↓ ↑
10÷5=2
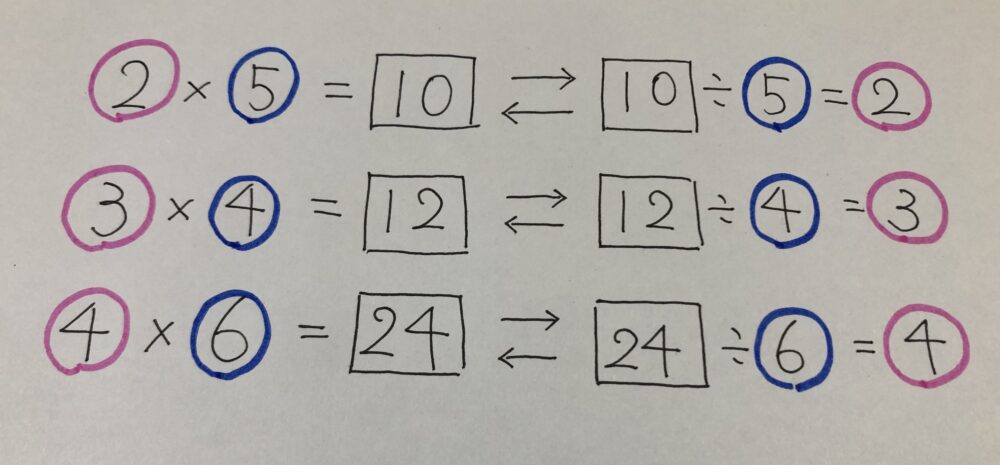
のように、かけ算とわり算には、
◯×△=⬜︎
↓ ↑
⬜︎÷△=◯
のように変形できる性質があります。これを「かけ算とわり算の式の性質」といいます。
「かけ算とわり算の式の性質」で、÷0の計算を考える
では、
10÷0=0が成り立つと仮定
して、この式を「かけ算とわり算の性質」を使って変形します。すると、
10÷0=0 → 0×0=10
となります。
0×0=10とはなりませんから、これは矛盾していることになります。
つまり、10÷0の計算の答えは0ではないことが「かけ算とわり算の式の性質」から説明できるのです。
÷0の計算の「答えがない」理由
では、10÷0の答えは一体いくつになるのかを考えていきましょう。
10÷0=?(?が正しい答え)とすると、「かけ算とわり算の性質」から、
10÷0=? → ?×0=10
となります。これを満たす「?」が10÷0の答えです。
もうおわかりでしょうか?「0をかけて10になる数」はありません。10の部分がどんな数であっても、×0をしてその数になることはありません。
だから、わられる数がいくつであっても、÷0の計算は「できない」、ということが説明できるのです。
÷0の答えは「無限♾️」なのでは?という問いはとても鋭い
以前担当していた生徒から、
「0はとても小さな数だから、÷0をすると答えは限りなく大きくなるはずでは?」
と質問をされたことがあります。これはとても鋭い質問です。
この考え方は「極限」という「限りなくある数に近づけていく」という数学的な考え方です。例えば、
- ÷0.01は×100
- ÷0.001は×1000
- ÷0.0001は×10000
というように、割る数を0に限りなく近づけていけばいくほど、かける数は大きくなっていきます。これを繰り返すと答えは「無限大♾️」となります。
割る数の小数点以下の0を増やしていけば0に限りなく近づき続け、それにともなってかける数は大きくなり続けるわけですから、÷0に近ければ近いほど答えは大きくなるだろうという考え方です。
この考え方は大正解です。しかし、これはあくまで
「限りなく0に近いが、0ではない数」
の話です。子どもの素朴な疑問から、教科書の範囲に関係なく、高校数学で扱う「極限」の分野にまで飛躍して考えさせることができました。他の興味を持った生徒にも説明してあげたところ、面白さに興奮していました。
まとめ
この記事を読んだ皆さんが、「なぜ÷0の計算できないのか」について納得して理解してくれたなら嬉しいです。
算数・数学の面白さは、「なぜそうなるのか?」を考えるところだと思います。この記事をきっかけに、
- 小中学生の授業で「÷0」について考えさせてみる
- お子様と一緒に他にも算数・数学の「なぜ?」を探してみる
などしても面白いと思います。もしよろしければ以下の記事もお読みください。
最後までお読みいただきありがとうございました。





