３×５＝１５は、正解
５×３＝１５は、不正解
のように、かけ算の文章題の解答で（かける数）と（かけられる数）を逆にしたことで不正解にされるということがSNSなどで話題になります。
いわゆる「かけ算の順序問題」です。
この記事では、
- 学習塾での指導
- 中学校数学科教員
- 小学校教員
の経験のある私が、
かけ算に順番は関係あるのか？という「掛け算の順序問題」について書いていきます。
「かけ算の順序問題」での２つの意見
まずは、「かけ算の順序問題」についての２つの意見について確認していきます。
式の順番が大切だという「順序肯定派」
式の順番が大切だという「順序肯定派」です。
テストで式の順序が違うことを不正解とする先生は、この立場の方かと思います。
このような「順序肯定派」の意見としてSNSなどに挙げられている理由としては、
- かけ算の意味を指導する上で重要だ
- 「いくつ分」ということを意識させることにつながる
- 教科書にもそう書いてある
などがあります。
式の順番はどちらでも良いという「順序否定派」
一方こちらは、式の順番はどちらでも良いという「順序否定派」です。
式の順番が違うという理由で不正解にしてしまうことに対し、否定的な考え方をする方々はこの立場です。
「順序否定派」の意見としては、
- 数学的に考えて順序は関係ない
- こんな指導は学校教育のみで行われているものだ
- 子どもの考えを狭めてしまうことになる
などが挙げられます。
ここから記事を書き進めていくにあたり、私の立場をハッキリさせておきます。
私は、こちらの「式の順序否定派」です。もっと簡単に言うと、
式の順序は「どっちでもいい派」
です。
以下、私がそのように考える理由を書いていきます。
そもそも「かけ算」とは？
この問題を考えるには、そもそも、かけ算とは何かという所から考える必要があります。
初めてかけ算を学習する小学２年生では、かけ算のことを
（〇つのまとまり）の（□つ分）
と学習します。
つまり、「数のまとまりに注目して、それがいくつ分あるか」を表したものがかけ算だというわけです。これが、本来のかけ算の意味ということになります。
式の順序によって採点で「×」をつける方は、この考え方に従って採点していると考えられるでしょう。
場面ごとに「数のまとまり」に着目して式の立て方を考える
式の立て方については、
「（数のまとまり）の（いくつ分）か」ということに注目して考えていく必要があります。問題の場面別に、考えていきましょう。
ものの個数を数える場面
まずは「ものの個数を数える場面」で考えます。「縦に３つ、横に５つ並んでいるチョコレートがあります。全部でいくつありますか？」という問題を例に考えてみましょう。
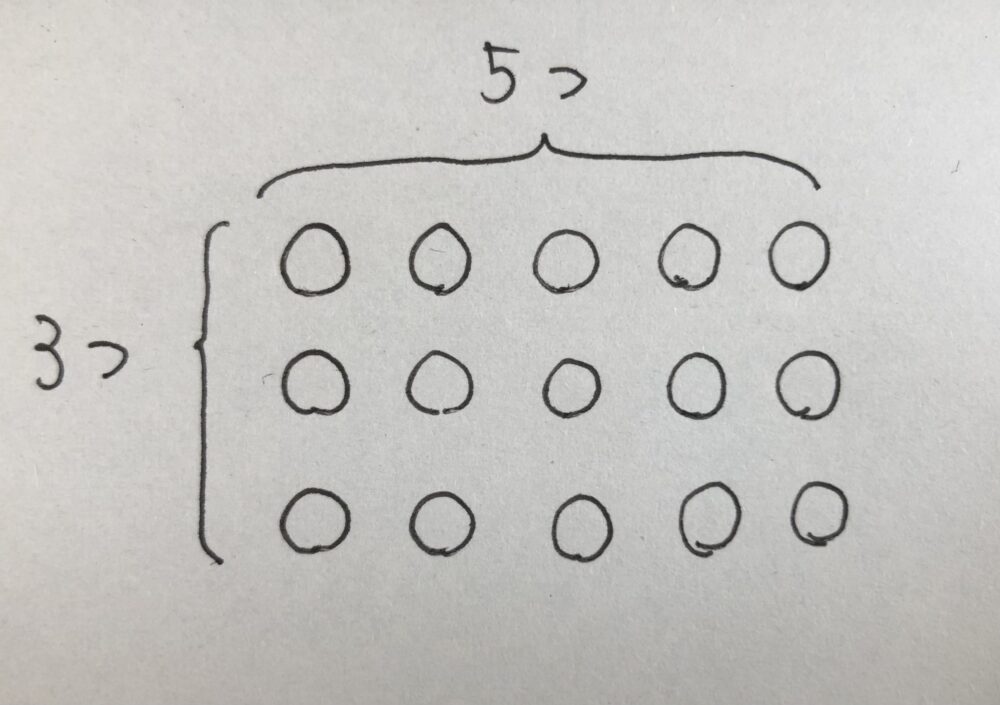
下のイラストを見てください。この問題の場合、
左の写真のように、「３つのまとまりが、５つ分」と考えれば「３×５」
右の写真のように「５つのまとまりが、３つ分」と考えれば「５×３」
という式で表すことができます。
 |  |
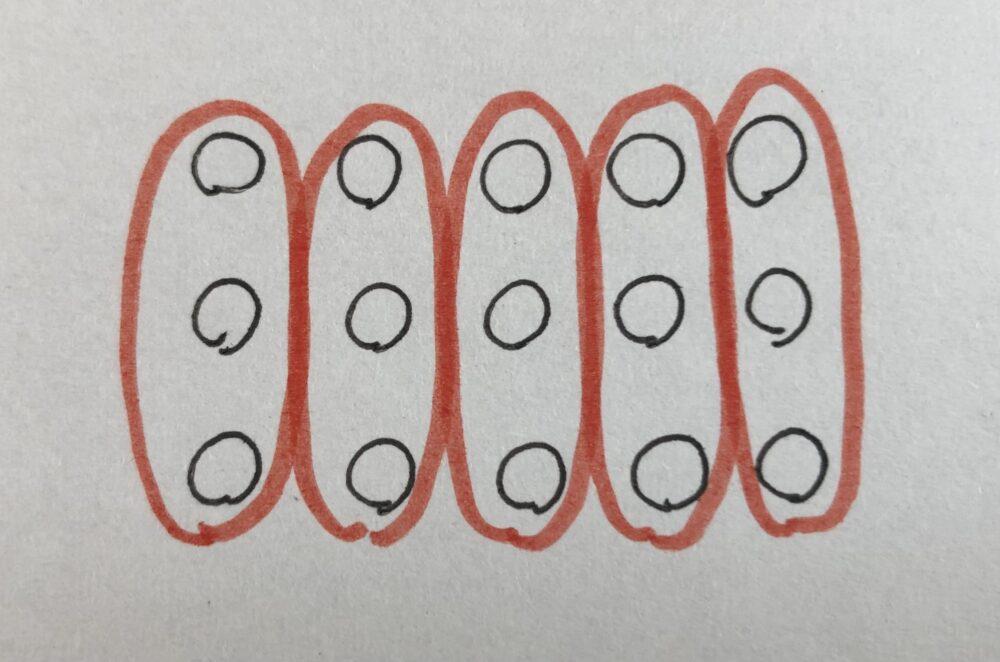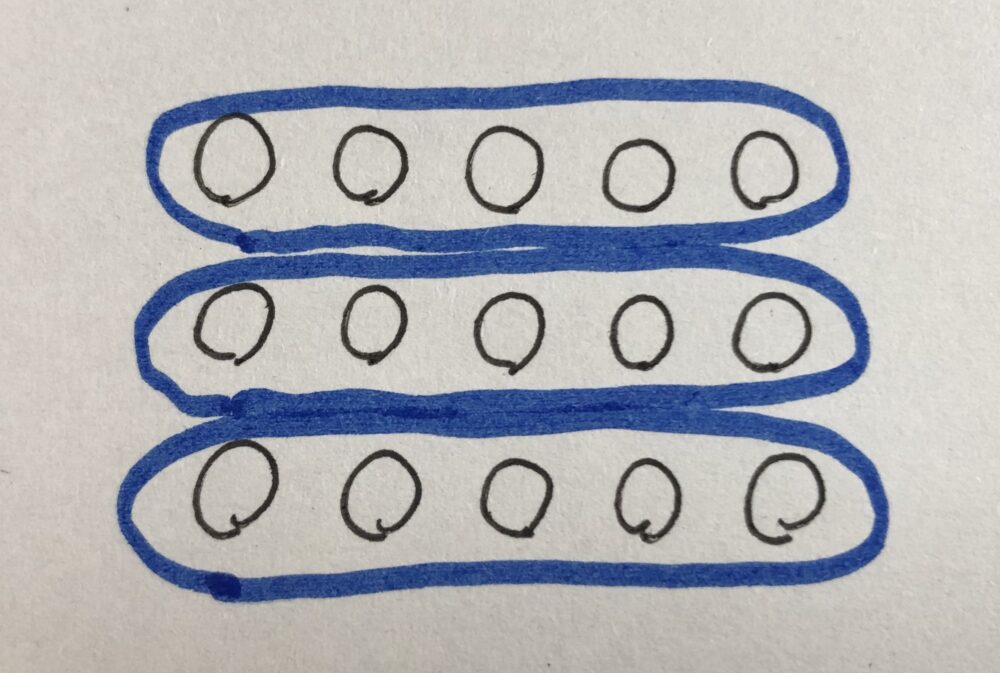このように「ものの数を数える場面」では、どこをまとまりとして考えるのかは様々ありますので、
私は「３×５＝１５」「５×３＝１５」のどちらも「○」であり、「×」にすべきではないと考えます。
面積を求める場面
次に、面積を求める場面を考えます。具体的に「縦３cm、横5cmの長方形の面積を求めましょう」という問題で考えていきます。
面積は１\(cm^2\)がいくつ分かを表すものですから、この場合、「縦３つ、横５つ並んでいるものの数を数える」という意味ではものの個数を数えること同じと考えられます。
しかし、ここでよく話題に上がるのは
「面積＝縦×横」
という「公式」の存在です。「公式」は「縦×横」ですから、公式をきちんと覚えさせるためには「３×５だけを〇にすべき」だという意見があります。実際、私の周りにもそう考える同僚がいました。しかし、私は「公式の理解」ということを考えればむしろ〇にすべきだと思います。
なぜなら、縦×横という公式はそもそも、１\(cm^2\)がいくつ分かを数えるための式であり、図形の見方を変えれば縦と横は変わりうるからです。
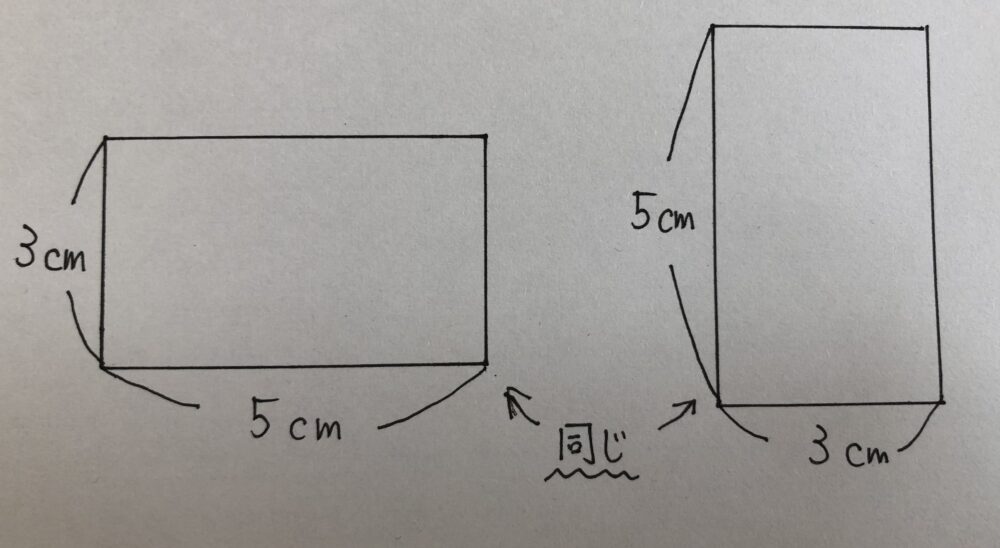
写真のように図形の見方を変えるだけで縦と横は逆になります。ですから、「面積」を求める場面においては「ものの数を数える場面」と同様に、
「３×５＝１５」「５×３＝１５」どちらも正答にすべきだと考えます。
「〇円のものを□こ買う」という場面
次に、「〇円のものを□こ買う」という場面を例に挙げます。このパターンが一番意見がわかれるケースではないでしょうか。「１つ３円のものを、５つ買ったときのねだんはいくらですか？」という問題を例に考えます。
この場面では、
３円というまとまりが５つ分
と考えて、３×５＝１５
というのが教科書的な模範解答です。では、この問題で「５×３＝１５」と書いた場合をどうするか…？ここが意見が分かれるところなのではないでしょうか。
数のまとまりに着目できていない可能性に注意する
上で挙げた「１つ３円のものを、５つ買ったときのねだんはいくらですか？」
という問題で５×３＝１５と書いた場合について、もう少し考えていきます。
このケースで考えるべきは、子どもが「数のまとまり」に着目できていない可能性があるという点です。
「５×３」という立式をした場合の可能性の一つとして、「３円というまとまり」に着目できていないことが考えられます。
「３円のものが５つ」と考えるべきところを「５円のものが３つ」と間違ってとらえている可能性もあります。
この場合、１５円という答えは同じでも、式が表す意味は違っているかもしれません。
そうだとするならば、子どもの理解を促すためという採点の意味合いを考えれば「×」をつけたくなる気持ちもわかります。しかし、私はこのような場合でも「〇」をつけています。
式だけで子どもの理解度を完全に把握することは不可能
私がなぜそのようなケースでも「〇」にしているかというと、そもそも「式だけで子どもの理解度を完全に把握することは不可能」だと考えるからです。
例えば「３×５」といわゆる教科書通りの回答をした場合でも、それは本当に「３円という数のまとまり」に着目してしているのかどうかは分かりようがないのです。
問題文の「３」と「５」という数をよく意味の分からないままかけ算の式にしただけの子がいたとして、その子が50%の確率で「○」になったり「×」になったりしてしまうのはどうなのでしょう？
逆に、「かけ算の交換法則」をしっかりと理解している子が、そのことまで考慮した上で「５×３」と解答している可能性だってあります。もしそうなら、理解度が一歩先に進んだ解答という可能性もあります。
大切なのは「かけ算を使う」ということが理解できているか
少し視点を変えると、本当に重要なのは式の順序よりも「かけ算を使う」ということの理解です。後々大切になってくるのは「かけ算なのか、わり算なのか」の理解です。
だから、少し乱暴な言い方をすれば、たとえかけ算の順番が違っていても「かけ算を使う」ということがわかっていれば◯で良いのではないでしょうか？
日常的に子どもに式の意味を問い、議論する場をつくることが必要
そもそも、テストはあくまで子どもの力をつけるためのものです。ですから、「〇」「✖️」よりも、なぜそうなるのか、なぜそうしたのかが大切です。
わたしは、その考えのもと「採点自体は〇」とした上で、「これは、どう考えて立式したのか？」などを直接聞くようにしています。そのために私は、採点を一人一人の子どもの目の前で行って、アドバイスしながら返却する場を設定しています。以下の記事では、そのような取り組みについて書いています。
また、日々の授業で
- なぜそうしたのか？
- 式の順序を逆にするとどうなるのか？
などを積極的に取り上げ、議論することを大切にしています。採点方法よりも、むしろそちらの方が大切だと思います。
また、採点を窮屈にしすぎると、算数・数学の自由さを奪うことにもなってしまうとも考えています。子どもが楽しく立式し、課題を解決することが大切だと思うので、あまり窮屈にしたくないというのも「〇」にする理由です。
まとめ
採点の「○」「×」については意見が分かれるところですが、大切なのは論争に決着がつくことではなく、
「子どもが何を学ぶか？」
です。私はこの「かけ算の順序問題」に関して「順序はどっちでもいい派」ですが、この記事によってそれが正しい意見であると主張したいわけではありません。
大切にすべきなのは、日頃から「なぜ？」と子どもたちに問うことで、子どもたちが式などの意味について考え議論する場を設定していくことなのではないでしょうか。
最後までお読みいただきありがとうございました。
